
前言
众所周知,《剑指offer》是一本“好书”。
为什么这么说?
因为在技术面试中,它里面罗列的算法题在面试中出现的频率是非常非常高的。
有多高,以我目前不多的面试来看,在所有遇到的面试算法题中,出现原题的概率大概能有6成,如果把基于原题的变种题目算上,那么这个出现概率能到达9成,10题中9题见过。
至于为什么给“好书”这两个字打引号,因为这本书成了面试官的必备,如果考生不会这本书上的题目,就很可能得到面试官负面的评价。这本书快要成为评判学生算法能力的唯一标准,这使得考前突击变成了一个惯例,反而让投机倒把成了必要,并不一定能真正的考察考生的算法能力。
对于剑指offer题解这个系列,我的写文章思路是,对于看了文章的读者,能够:
- 迅速了解该题常见解答思路(奇技淫巧不包括在内,节省大家时间,实在有研究需求的人可以查阅其它资料)
- 思路尽量贴近原书(例如书中提到的面试官经常会要求不改变原数组,或者有空间限制等,尽量体现在代码中,保证读者可以不漏掉书中细节)
- 尽量精简话语,避免冗长解释
- 给出代码可运行,注释齐全,对细节进行解释
快速找到我的《剑指offer题解》专栏:
- 公众号(Rude3Knife):底部导航栏——剑指offer题解
- CSDN(@Rude3Knife):剑指offer题解专栏
题目介绍
剑指offer面试题59题
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个: {[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
解题思路
蛮力法
思路
扫描窗口k,得到最大值。对于长度为n的数组,算法时间复杂度O(nk)
显然不是最优解。
用两个栈实现队列
思路
面试题30中,我们实现过用两个栈实现了队列,可以在O(1)时间得到栈的最大值,也就可以得到队列的最大值。
这样总的时间复杂度O(n)
但是这样的思路写代码,等于同时要写两个题目,面试时间可能不允许。
双端队列
思路
参考解释:
https://cuijiahua.com/blog/2018/02/basis_64.html
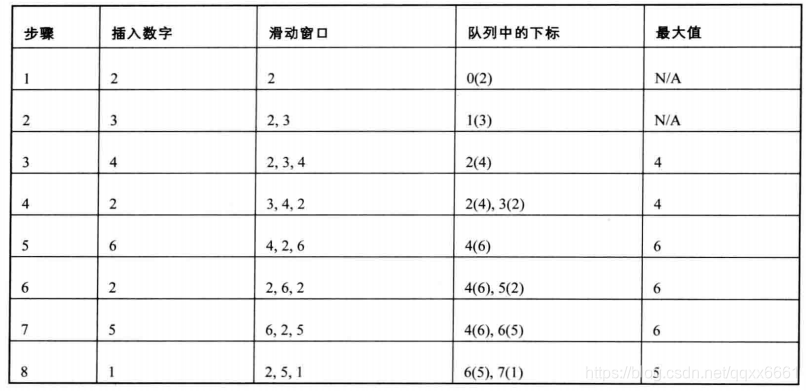
数组的第一个数字是2,把它存入队列中。第二个数字是3,比2大,所以2不可能是滑动窗口中的最大值,因此把2从队列里删除,再把3存入队列中。第三个数字是4,比3大,同样的删3存4。此时滑动窗口中已经有3个数字,而它的最大值4位于队列的头部。
第四个数字2比4小,但是当4滑出之后它还是有可能成为最大值的,所以我们把2存入队列的尾部。下一个数字是6,比4和2都大,删4和2,存6。就这样依次进行,最大值永远位于队列的头部。
但是我们怎样判断滑动窗口是否包括一个数字?应该在队列里存入数字在数组里的下标,而不是数值。当一个数字的下标与当前处理的数字的下标之差大于或者相等于滑动窗口大小时,这个数字已经从窗口中滑出,可以从队列头部把它删除。因此,我们既有可能从头部删除数字,又可能从尾部删除数字,所以要双端队列。
代码
注意点:
ArrayDeque的几个API:pollFirst、peekFirst等
ArrayDeque保存的是下标
最新的数的下标是必定加进去的。
1 | import java.util.ArrayList; |
总结
采用双端队列,非常巧妙地一题。
关注我
我目前是一名后端开发工程师。技术领域主要关注后端开发,数据爬虫,数据安全,5G,物联网等方向。
微信:yangzd1102
Github:@qqxx6661
个人博客:
原创博客主要内容
- Java知识点复习全手册
- Leetcode算法题解析
- 剑指offer算法题解析
- SpringCloud菜鸟入门实战系列
- SpringBoot菜鸟入门实战系列
- Python爬虫相关技术文章
- 后端开发相关技术文章
个人公众号:Rude3Knife

如果文章对你有帮助,不妨收藏起来并转发给您的朋友们~